Wprowadzenie do przetwarzania obrazów

Politechnika Poznańska, Instytut Robotyki i Inteligencji Maszynowej

Ćwiczenie laboratoryjne 5: Wykrywanie krawędzi

Powrót do spisu treści ćwiczeń laboratoryjnych

Pochodne cząstkowe

Obraz cyfrowy może być traktowany jako dwuwymiarowa funkcja dyskretna. Wszelkiego rodzaju krawędziom na obrazie towarzyszy zmiana wartości intensywności obrazu. Do wyliczenia pochodnych cząstkowych można wykorzystać maski Prewitta (dla zmian pionowych i poziomych) lub Sobela (dla zmian skośnych).

• Maska Prewitta

  Umożliwia obliczenie pochodnych w dwóch podstawowych kierunkach. \[ \mathbf{M_x} = \begin{bmatrix} 1 & 0 & -1 \\\\ 1 & \underline{0} & -1 \\\\ 1 & 0 & -1 \end{bmatrix}, \mathbf{M_y} = \begin{bmatrix} 1 & 1 & 1 \\\\ 0 & \underline{0} & 0 \\\\ -1 & -1 & -1 \end{bmatrix} \]

  Pochodne kierunkowe uzyskuje się poprzez splot obrazu z odpowiednią maską i podzielenie wyniku przez 3.

• Maska Sobela

  Podobnie jak maska Prewitta umożliwia obliczenie pochodnych w dwóch podstawowych kierunkach, jednak waga centralnego wiersza lub kolumny jest wyższa. \[ \mathbf{M_x} = \begin{bmatrix} 1 & 0 & -1 \\\\ 2 & \underline{0} & -2 \\\\ 1 & 0 & -1 \end{bmatrix}, \mathbf{M_y} = \begin{bmatrix} 1 & 2 & 1 \\\\ 0 & \underline{0} & 0 \\\\ -1 & -2 & -1 \end{bmatrix} \]

Pochodne kierunkowe uzyskuje się poprzez splot obrazu z odpowiednią maską i podzielenie wyniku przez 4. Przykładowy obraz i wartości bezwzględne gradientów wyznaczone filtrem Sobela przedstawiono poniżej.

💥 Zadanie do wykonania 💥

Napisz program umożliwiający wczytanie pliku graficznego w skali szarości, a następnie obliczenie pochodnych cząstkowych za pomocą maski Prewitta i Sobela (należy wykorzystać funkcję cv2.filter2D).

Uwaga:
Wykorzystaj typ np.float32 w celu przechowania wyników działania funkcji cv2.filter2D. Dokumentacja dla funkcji.

Moduł i kierunek gradientu

Jednym ze sposobów śledzenia zmian jasności na obrazie jest analiza gradientu funkcji obrazowej (zarówno jego modułu jak i orientacji). Operator gradientu funkcji dwuwymiarowej można przedstawić w następujący sposób: \[ \nabla=\left[\begin{array}{c} \frac{\delta}{\delta x} \\ \frac{\delta}{\delta y} \end{array}\right] \]

Po zastosowaniu go do funkcji przybiera formę:

\[ \nabla \mathrm{f}=\left[\begin{array}{c} \frac{\delta}{\delta x} f \\ \frac{\delta}{\delta y} f \end{array}\right] \]

Dla tak zdefiniowanego gradientu można (jak dla każdego wektora) określić moduł \(\|\nabla f\|\) i orientację \(\Phi(\nabla f)\). Wartość modułu daje informację o sile krawędzi, a orientacja o jej kierunku (wskazuje kąt prostopadły do krawędzi). Z faktu, że różniczkowanie jest operacją ciągłą, a obrazy są dwuwymiarową funkcją dyskretną wynika konieczność aproksymacji różniczkowania. Operacja różniczkowania jest liniowa i niezależna od przesunięcia, dlatego zazwyczaj realizuje się ją przez splot z odpowiednią maską.

Moduł gradientu wyznacza się jako pierwiastek z sumy kwadratów pochodnych kierunkowych. Łączy on informację o gradientach cząstkowych w punkcie obrazu. Kierunek gradientu wyznacza kierunek spadku funkcji obrazowej w punkcie. Moduł i kierunek gradientu wyrażone są wzorami:

\[ \begin{array}{c} M(x, y)=\sqrt{M_{x}(x, y)^{2}+M_{y}(x, y)^{2}} \end{array} \]

\[ \begin{array}{c} \theta(x, y)=\arctan \left(\frac{M_{y}(x, y)}{M_{x}(x, y)}\right) \end{array} \]

💥 Zadanie do wykonania 💥

Dla wyliczonych wcześniej pochodnych, oblicz i wyświetl obraz modułu gradientu.

Uwaga:
Przed wyświetleniem należy przeskalować zakres wartości do 0..255 - w tym celu wykorzystaj funkcję np.amax. Następnie przekonwertuj obraz do uint8 korzystając z metody astype.

Wykrywanie krawędzi - metoda Canny’ego

Efekt zastosowania większości detektorów opartych o gradient jest niezadowalający. Aby wykryć krawędzie należy progować uzyskany wynik. Zbyt niski próg prowadzi do powstania wielu artefaktów, zbyt wysoki powoduje przerywanie segmentów. Problem ten jest częściowo rozwiązany przez zastosowanie detektora Canny’ego. Jego działanie można podzielić na 4 etapy:

• Wygładzanie - obraz wejściowy jest wygładzany za pomocą filtru Gaussowskiego.

• Wyznaczanie gradientu - wyznaczany jest moduł gradientu obrazu.

• Tłumienie wartości niemaksymalnych - wartości gradientu prostopadłe do krawędzi są tłumione. Przez “prostopadłe” rozumie się tu leżące w kierunku gradientu. W ten sposób wygaszane są wszystkie punkty, które nie leżą na grzbiecie wyznaczonego obrazu modułu gradientu.

  

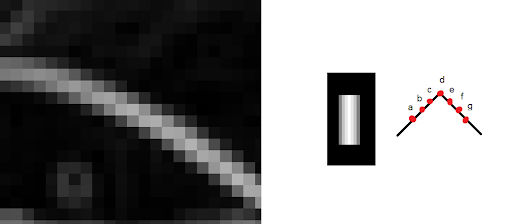
• Uciąglanie - wykrywanie krawędzi działa na zasadzie histerezy. Określane są dwa progi. Piksele o wartości modułu gradientu większej od większego progu są automatycznie traktowane jako krawędzie. Piksele o wartości modułu mniejszej od mniejszego progu są automatycznie odrzucane. Piksele wartości modułu znajdującej się pomiędzy progami są akceptowane tylko jeżeli sąsiadują z pikselem należącym do krawędzi.

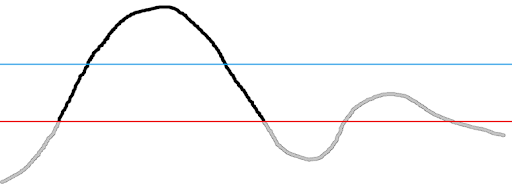
  Dla zilustrowania przedstawiono poniżej przebieg wartości funkcji. Jeśli kolorem niebieskim oznaczymy próg wyższy, a czerwonym próg niższy, wartości oznaczone na czarno zostaną pozostawione, szare - odrzucone.

  

W praktyce kroki 1 i 2 są wykonywane równocześnie przez zastosowanie operatora Sobela.

💥 Zadanie do wykonania 💥

Napisz program wykrywający krawędzie w obrazie metoda Canny’ego (należy wykorzystać funkcję cv2.Canny). Zbadaj wpływ różnych ustawień progów. Do wybierania poziomu progów wykorzystaj poznaną wcześniej fukcjonalność suwaków (trackbar).

Wykrywanie linii prostych oraz okręgów przy pomocy transformaty Hough’a

Wykrycie prostej linii na obrazie może w znaczący sposób uprościć jego analizę. Jedną z metod stosowanych do detekcji linii prostych w obrazie jest transformata Hough’a. Zakłada ona, że przez każdy punkt obrazu przechodzi nieskończenie wiele prostych opisanych równaniem:

\[ \rho=x \cos (\theta)+y \sin (\theta) \]

Zilustrowano to na rysunku poniżej:

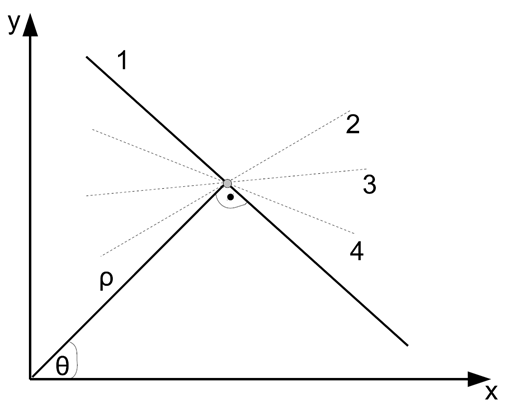
Każdej linii odpowiada jeden punkt w przestrzeni parametrów \(\rho\), \(\theta\), bo dla każdej linii mamy jedną, unikalną parę wartości tych parametrów. Linie przechodzące przez ten sam punkt są zmienne tylko ze względu na parametr \(\theta\), więc wszystkie linie przechodzące przez punkt tworzą w przestrzeni parametrów sinusoidę. Można więc powiedzieć, że reprezentacją punktu w przestrzeni obrazu jest w przestrzeni parametrów sinusoida.

Odwróćmy teraz sytuację. Jeśli mamy punkt w przestrzeni parametrów \(\rho\), \(\theta\), co jest jego reprezentacją w przestrzeni obrazu? Ustalenie każdego z parametrów \(\rho\) i \(\theta\) na pewną stałą wartość daje nam w dziedzinie zmiennych \(x\) i \(y\) równanie funkcji.

Załóżmy teraz, że wyznaczyliśmy algorytmem Canny’ego krawędzie w obrazie. Dla każdego punktu krawędzi o współrzędnych x i y wyznaczamy reprezentację w przestrzeni parametrów. Każdą tak wyznaczoną reprezentację akumulujemy (nowy stan akumulatora = stary stan akumulatora + reprezentacja w przestrzeni parametrów).

Przykładem wykonania transformaty dla wszystkich punktów obrazu (w przestrzeni parametrów \(\rho\), \(\theta\)) jest wykres jak na rysunku poniżej:

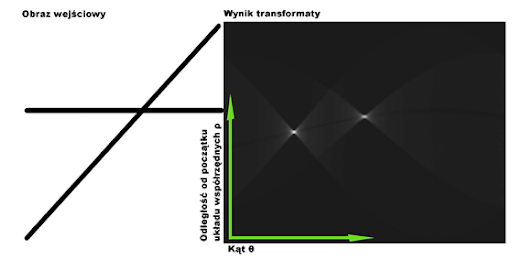
Liczba pikseli dzielących taki sam wzór prostej przedstawiona jest jako jasność w obrazie. Punkty o największej jasności to te, dla których istnieje najwięcej punktów wspierających. Dlatego właśnie obraz wyniku transformaty nazywa się akumulatorem, a metodę wyboru głosowaniem.

Detekcji okręgów dokonuje się w podobny sposób, co detekcji prostych. Do opisu okręgu wykorzystuje się trzy parametry \((x, y, r)\) zgodnie z równaniem:

\[r^{2}=(a-x)^{2}+(b-y)^{2}\]

Gdzie \(a\) i \(b\) to zmienne, \(r\) to promień okręgu, a \(x\) i \(y\) to współrzędne jego środka.

💥 Zadanie do wykonania 💥

Napisz program wykrywający w obrazie linie proste oraz okręgi (wykorzystać funkcje HoughLines, HoughLinesP, HoughCircles). Do testów można wykorzystać obraz shapes.jpg. Jako wzór wykorzystaj tutorial dla linii oraz dla okręgów.

Uwaga!
Zwróć szczególną uwagę na to jak zwracane są położenia wykrytych linii i okręgów - przyda się to w kolejnych zadaniach.

Zadania do samodzielnej realizacji

💥 Zadanie do wykonania 💥

Napisz program, który możliwie dobrze nakreśli granice statku na zdjęciu dla autonomicznie lądującej rakiety. Wykorzystaj jako wejście obraz drone_ship.jpg.

💥 Zadanie do wykonania 💥

Napisz program oznaczający automatycznie pomarańcze i jabłka dla sortowni owoców. Wykorzystaj jako wejście obraz fruit.jpg. Dla robota zbierającego wystarczy, że owoce dwóch rodzajów będą otoczone obwódkami w różnych kolorach.

💥 Zadanie do wykonania 💥

Policz automatycznie jaka kwota znajduje się na obrazie coins.jpg. Sumę monet wyświetl w terminalu z dokładnością do 2 miejsc po przecinku, wykorzystując f-string.